Secteur sphérique

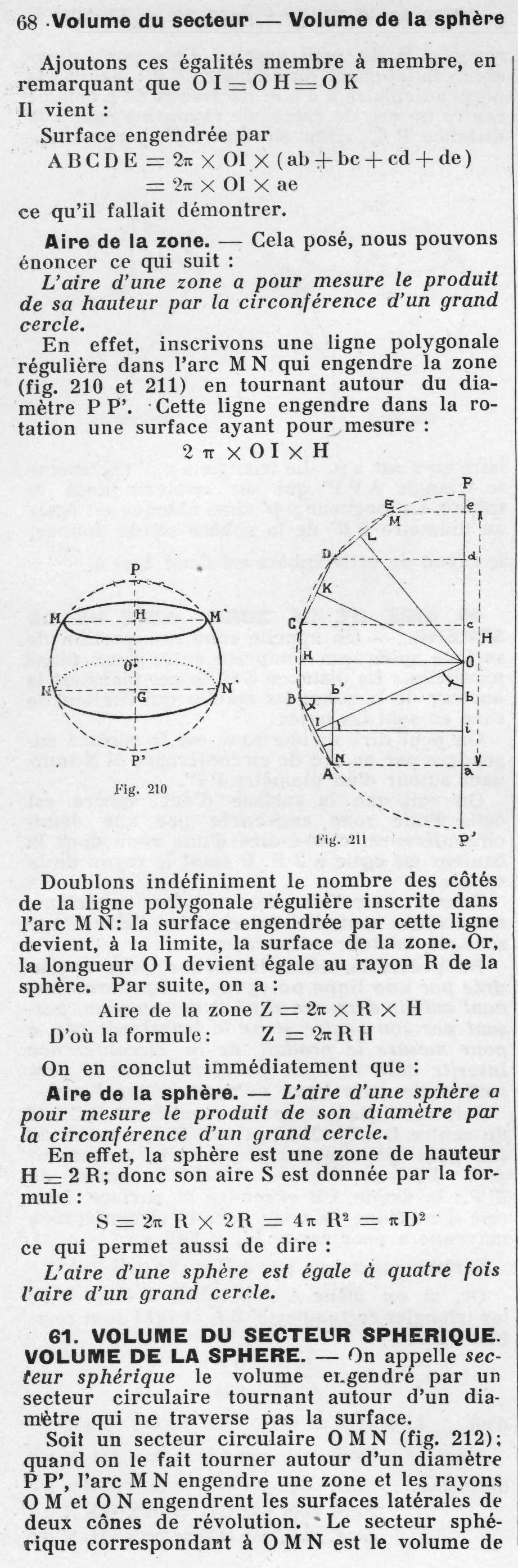
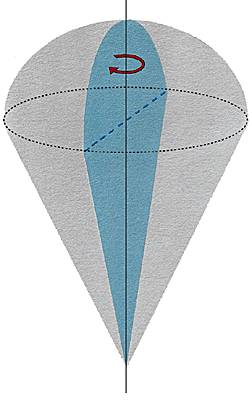
En géométrie, un secteur sphérique est une portion de sphère - plus exactement de boule - délimitée par un demi-cône de révolution dont le sommet coïncide avec le centre de la sphère.

C'est un solide de révolution dont la frontière est constituée d'une portion de cône et d'une calotte sphérique.

Plus précisément, le demi-cône découpe dans la boule deux solides, l'un, convexe, dont le volume est inférieur à une demi-boule est appelé secteur mineur, l'autre est appelé secteur majeur. C'est le secteur mineur que l'on appelle communément secteur sphérique.

Ne pas confondre: les vannes dites à secteur sphérique en robinetterie sont en réalité composées à l'aide d'une portion de sphère creuse proche d'un fuseau sphérique.

Volume

Si on note r le rayon de la sphère et h la hauteur de la calotte sphérique, le volume du secteur sphérique est: $V={\frac {2\pi r^{2}h}{3}}\,.$

Ce volume peut également s'exprimer à l'aide de l'angle au sommet φ du cône (c'est-à-dire l'angle entre l'axe de rotation du cône et une de ses génératrices) : $V={\frac {2\pi r^{3}}{3}}(1-\cos \varphi )\,.$

Enfin, ce volume est entièrement déterminé par le rayon r de la sphère et l'aire A' de la calotte sphérique par la formule: $V={\frac {rA'}{3}}\,.$

Il est lié à l'angle solide $\Omega$ du cône par la formule : $V=\Omega {\frac {r^{3}}{3}}$

Le théorème de Guldin permet de relier ce volume avec l'aire s et le centre de gravite G' du secteur circulaire engendrant par rotation le secteur sphérique. Si d est la distance entre G' et l'axe de rotation on a : $V=2\pi \times s\times d\,,$ avec $s={\frac {1}{2}}r^{2}\theta \,,$ $MG'={\frac {2}{3}}{\frac {\sin(\theta /2)}{\theta /2}}\cdot r\,,$ $d=MG'\times \sin(\theta /2)={\frac {2}{3}}{\frac {1-\cos \theta }{\theta }}\cdot r\,.$ Ce qui donne : $V=2\pi \times {\frac {1}{3}}(1-\cos \theta )r^{3}\,.$

Aire

L'aire de la surface enveloppant le secteur sphérique est constituée de la somme de l'aire de la surface conique et de l'aire A' de la calotte sphérique: $A=\pi ra 2\pi rh=\pi r(a 2h)\,,$ où a est le rayon du cercle faisant la jonction entre les deux surfaces.

Centre de gravité

Comme dans tout solide de révolution, le centre de gravité G d'un secteur sphérique est situé sur l'axe de révolution. Il est à une distance du centre M donnée par la formule: $MG={\frac {3}{8}}(2r-h)\,.$

Calcul intégral

En coordonnées sphériques, le volume peut être calculé en intégrant l'élément de volume $dV=\rho ^{2}\sin \phi \,d\rho \,d\phi \,d\theta$ avec

$\theta$ variant de 0 à 2π
$\rho$ variant de 0 à r
$\phi$ variant de 0 à φ où φ est l'angle au sommet du cône (c'est-à-dire l'angle entre l'axe de rotation du cône et une de ses génératrices)

V=\int _{0}^{2\pi }\int _{0}^{\varphi }\int _{0}^{r}\rho ^{2}\sin \phi \,d\rho \,d\phi \,d\theta =\int _{0}^{2\pi }d\theta \times \int _{0}^{\varphi }\sin \phi \,d\phi \times \int _{0}^{r}\rho ^{2}\,d\rho =2\pi \times \left[\cos \phi \right]_{0}^{\varphi }\times \left[{\frac {\rho ^{3}}{3}}\right]_{0}^{r}={\frac {2\pi r^{3}}{3}}(1-\cos \varphi )\,.

L'intégrale a pu être décomposée en un produit de trois intégrales car l'intégrande est composé d'un produit de trois termes contenant chacun une seule variable.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Spherical sector » (voir la liste des auteurs).